TAChart Tutorial: Function Series

│ English (en) │ suomi (fi) │

Introduction

Did you work through the Getting started tutorial? In that tutorial we had used some mathematical functions to demonstrate the basic usage of TAChart by means of line series. Line series, however, is not the best choice for drawing mathematical functions. TFuncSeries is much better suited to this purpose. This is a series type that -- at first sight -- looks like an ordinary line series. But in the background, it is completely different. It does not get its data from a ChartSource, but from a mathematical function. Whenever the series needs data it calls the handler for OnCalculate event where the user can pass the function values for an x value requested. This saves memory for storage of the function values. But most of all, it allows to calculate the function values, depending on zooming level and chart size, at sufficiently narrow intervals, such that the series curve is smooth even at high magnifications.

Preparation

Let us start a new project with a standard TChart component on the main form. Modify its properties as you like. We will use the following settings for the rest of this tutorial:

• Align: alClient
• BackColor: clWhite
• BottomAxis: Grid.Color = clSilver, Title.Caption = 'x', Title.Visible = true, Title.LabelFont.Style = fsBold
• LeftAxis: Grid.Color = clSilver, Title.Caption = 'y', Title.Visible = true, Title.LabelFont.Style = fsBold

The resulting form is displayed in the following image on the left:

Adding a TFuncSeries

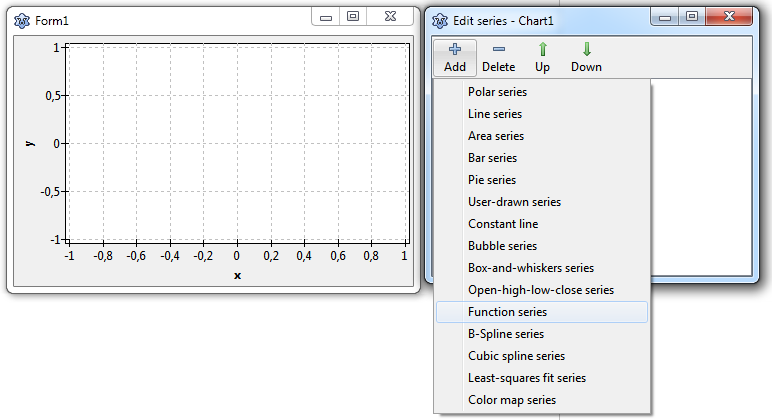
At first, let's draw a sine function, y = sin(x). We double-click on the chart, the series editor opens ("Edit series"). Click on "Add" and select "Function series" from the drop-down list. The chart will display a line going from the bottom-left to the top-right corner as a representative of the FuncSeries.

We could give the series a red color. Function series don't have a SeriesColor property, but we can use the property Pen for this purpose: Set Pen.Color to clRed.

Now we go to the page "Events" of the object inspector, and double-click on the event OnCalculate. This is the place where we define the function. OnCalculate is called whenever the series needs the y value for a given x value:

procedure TForm1.Chart1FuncSeries1Calculate(const AX: Double; out AY: Double);
begin
  AY := sin(AX);
end;

When we compile we'll see the sine funtion. But it is not the full wave - because we did not set up the axes, x runs only between -1 and +1, the default for an empty x axis extent.

Setting the extent

x extent

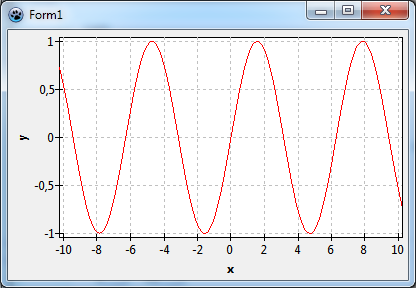
To get a wider axis range we have two options: we can set the extent of the series or the extent of the chart. There are subtle differences between both cases, in our simple chart, however, they won't show up, and therefore, we will not discuss them here. So go to the object inspector, select the series' property Extent, set the axis start at XMin to, say, -10, and the axis end at XMax to +10. Activate these axis limits by setting UseXMin and UseXMax to true. Now when you recompile, you'll see the sine function between -10 and 10.

y extent

Why don't we play with the function a bit to see what happens? Go to the OnCalculate event handler again and multiply the sine function by 2:

procedure TForm1.Chart1FuncSeries1Calculate(const AX: Double; out AY: Double);
begin
  AY := 2*sin(AX);
end;

Oh -- the function series does not automatically update the y extent! This is true for the release version of Lazarus v1.0. In the trunk version, however, the FuncSeries has a new property ExtentAutoY which, if set to true, enforces automatic calculation of the y extent. Please note that the property applies only if both Extent.UseXMin and Extent.UseXMax are true.

If you don't have the trunk version of Lazarus you have to set the extent manually: Select the series Extent again, set YMin to -2, YMax to 2, and UseYMin and UseYMax to true. This will show us the full sine curve with amplitude 2.

Zooming

Now let's focus on the statement in the introduction that function series are always smooth, even at high magnification. To see the difference, we plot the sine function a second time, but now as a line series which draws the function only with predefined segments.

Add a "line series" to the chart, set its Pen.Style to psDash, and add code to the form's OnCreate event handler which defines the series data:

procedure TForm1.FormCreate(Sender: TObject);
const
  N = 100;
  XMIN = -10;
  XMAX = 10;
var
  i: Integer;
  x: Double;
begin
  for i:=0 to N-1 do begin
    x := XMIN + (XMAX - XMIN) * i / (N-1);
    Chart1LineSeries1.AddXY(x, 2*sin(x));
  end;
end;

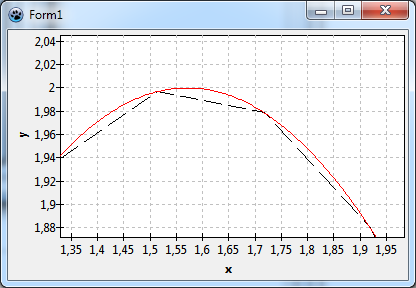
When you compile you'll see an overlay of the red function series and the black line series, the curves are hard to separate. Now zoom into the chart: while holding the left mouse button down drag a small rectangle near one of the maxima of the sine function (you need to drag from the top-left to the bottom-right corner to get the zoom effect). After you release the mouse you'll see a blow-up of the zoomed rectangle. If the magnification is large enough, you will see the segments of the line series, but the function series will still be smooth.

What is the reason why the function series is so smooth even at extreme magnification? This is because the function is calculated at very small intervals defined by the property Step of TFuncSeries. This number is in screen pixels and, therefore, the smoothness is independent of zoom magnification. Its default value of 2 is a good compromise between almost perfect resolution and drawing speed for most functions.

Before we continue, delete the line series -- we don't need it any more. Remove also the FormCreate event handler.

Domain exclusions

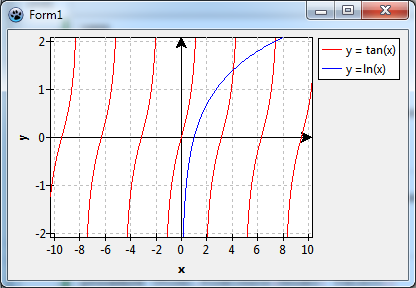
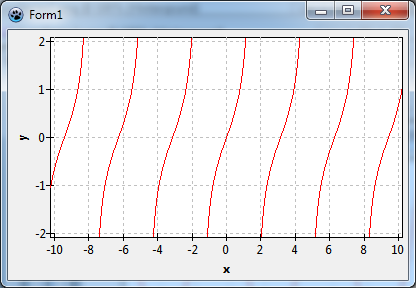
Plotting y = tan(x)

In this exercise we want to plot a different function, y = tan(x). We can easily adapt our project to this function by changing the OnCalculate event handler (you will need the math unit in the uses clause):

procedure TForm1.Chart1FuncSeries1Calculate(const AX: Double; out AY: Double);
begin
  AY := tan(AX);
end;

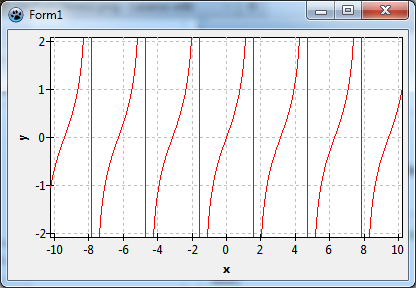
The chart looks fine at first sight, but when you remember some basics of the tan function from school you'll notice that the (almost) vertical lines near ±1.6, ±4.7, ±7.9 are not correct. The function is not defined at these locations (to be exact, at (n+1/2)π). The lines should not be there. Because the function series does not "know" about these discontinuities, it draws a connection line between the last and first calculated point before and after the discontinuities.

TFuncSeries provides so-called DomainExclusions to overcome this issue. These are points and regions at which the function is not calculated and not drawn. Presently, DomainExclusions do not appear in the Object Inspector, but must be assigned in code at runtime by calling their methods AddPoint or AddRange.

In case of the tan function, we add the following code to the form's OnCreate event handler in which we exclude above-mentioned points from the calculation:

procedure TForm1.FormCreate(Sender: TObject);
begin
  with Chart1FuncSeries1.DomainExclusions do begin
    AddPoint(pi/2);      AddPoint(-pi/2);
    AddPoint(3*pi/2);    AddPoint(-3*pi/2);
    AddPoint(5*pi/2);    AddPoint(-5*pi/2);
  end;
end;

This chart, now, is perfect.

It should be mentioned, however, that the code in the FormCreate procedure is too specific and is correct only for our x axis range from -10 to 10. Suppose the user could zoom out or could change the axis limits in some other way. Then these domain exclusions may not be appropriate any longer. Therefore, you should provide a more general method, maybe "UpdateDomainExclusions", and call it where appropriate. The first idea would be to use the chart's OnExtentChanged event. Without going into details, however, this may cause a hang under some circumstances because this event occurs after drawing of the chart. In Lazarus v2.1 or newer, however, there is a new event OnExtentValidate which is better suited because it is called before any drawing. If you stick to an older version you could use the event handler for TChart.OnAfterDrawBackwall although its name is not intuitive for this purpose. Don't forget to call DomainExclusions.Clear to avoid adding the same points again and again.

procedure TForm1.UpdateDomainExclusions;
var
  ex: TDoubleRect; // unit TAChartUtils.pas
  x: Integer;
begin
  ex := Chart1.CurrentExtent;
  Chart1.DisableRedrawing;
  try
    with Chart1FuncSeries1.DomainExclusions do begin
      Clear;
      for x := Floor(ex.a.x / Pi - 0.5) to Ceil(ex.b.x / Pi + 0.5) do
        AddPoint((x + 0.5) * Pi);
    end;
  finally
    Chart1.EnableRedrawing;
  end;
end;

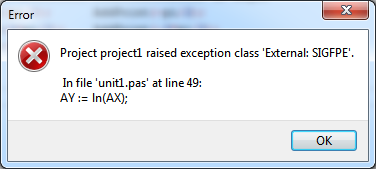
Plotting y = ln(x)

In the last exercise, we add another function, y = ln(x). For this, double-click on the chart again, and in the series editor add another function series. Set its color to clBlue, and write the following OnCalculate event handler which tells the series to plot a log function:

procedure TForm1.Chart1FuncSeries2Calculate(const AX: Double; out AY: Double);
begin
  AY := ln(AX);
end;

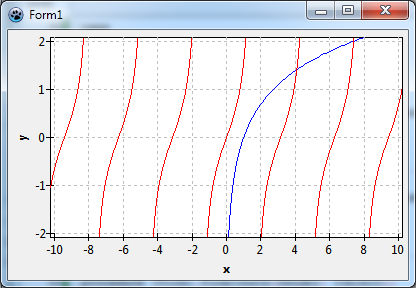
But when we run the program it crashes because of a floating point exception! Where does that come from? Our x axis starts at -10, and the logarithmic function can be calculated only for positive x values. What can be done against that? The answer is domain exclusions, again. We just forbid calculation of the function for negative values and for x = 0. This can be achieved by adding a range from -INF to 0 to the series' domain exclusions. The method AddRange, by default, also includes the end points of the interval, so we need no special treatment for x = 0. We modify the form's OnCreate event handler as follows:

procedure TForm1.FormCreate(Sender: TObject);
begin
  with Chart1FuncSeries1.DomainExclusions do begin
    AddPoint(pi/2);      AddPoint(-pi/2);
    AddPoint(3*pi/2);    AddPoint(-3*pi/2);
    AddPoint(5*pi/2);    AddPoint(-5*pi/2);
  end; // ... or use the UpdateDomainExclusions procedure discussed in the text
  with Chart1FuncSeries2.DomainExclusions do begin
    AddRange(NegInfinity, 0);
  end;
end;

Now the program runs fine.

What if we would want to plot the function y = sqrt(x)? There is a subtle difference to y = log(x): while both functions cannot be calculated for x < 0, sqrt(x) is defined also at x = 0, i.e. the point x = 0 must be excluded from the domain exclusion interval. This can be achieved in the AddRange method by specifying the open end(s) of the interval in an optional third parameter set of TIntervalOption = (ioOpenStart, ioOpenEnd). The correct code to set up the DomainExclusions for y = sqrt(x), therefore, is

  SqrtXSeries.DomainExclusions.AddRange(NegInfinity, 0, [ioOpenEnd]);

One thing to mention is the property Epsilon of the DomainExclusions. This value controls the distance between the endpoint of the excluded interval and the last drawn function point (of a closed excluded interval). Its default value of 1e-6 is fine for most cases, but you may want to change it if it does not lead to correct results.

Cleaning up

Legend

Before we finish we could apply some improvements. Never show several curves in the same chart without a legend, there would be no way to distinguish them. Enter the function names as the Title of both series, and set the legend's Visible to true.

Additional coordinate axes (TConstantLineSeries)

Plots of mathematical functions often have axes crossing at the origin. The trunc version of TAChart now has an option to shift the axes away from the chart edge by applying the new property Position. But maybe you prefer the release version 1.0? For this case let's go another way:

Open the series editor again, and add two "constant line" series. These are very simple series that display a line parallel to the coordinate axes. Their location is defined by the property Position, their direction -- horizontal or vertical -- by LineStyle. There is nothing to do with Position which has the default value 0. You just have to set LineStyle of the one series to lsHorizontal, and that of the other one to lsVertical. The TConstantLineSeries also has an arrow which can be activated by setting Arrow.Visible to true. Play with Length, Width and BaseLength properties of an Arrow to find the shape that you want.

Finally you should turn off the constant series' property Legend.Visible, otherwise there will be two unidentified entries in the legend.

Here's the final result:

Source code

The source code for the final version of this tutorial project can be found in the folder tutorials/func_series of the TAChart installation.